In this post, we will prove that the decision version of the set-covering problem is NP-complete, using a reduction from the vertex covering problem (which is NP-complete). This is Exercise 35.3-2 in CLRS3.
We will follow the template given in an earlier post.
Problem Statement
We seek to answer whether a set cover \(\mathcal{C}\) exists for \(X\) (the set containing the elements to be covered), containing a maximum of \(k\) sets.
Showing the problem is in NP
Let \(\mathcal{C} = \{S_1, S_2, \ldots, S_n\}\) be the certificate. We assume that each \(S \in \mathcal{C}\) uniquely covers at least one \(x \in X\), so:
\[ \begin{aligned} |\mathcal{C}| &\leq |X|\\ \forall S \in \mathcal{C} : |S| &\leq |X| \end{aligned} \]
This gives us that we can verify that \(n \leq k\) and that \(\mathcal{C}\) covers \(X\) in \(\mathcal{O}(|X|^2)\), which proves the problem is in NP.
Showing the problem is NP-hard
We will show that the decision version of the set-covering problem is NP-hard by showing:
\[ \text{Vertex-Cover} \leq_\text{P} \text{Set-Cover} \]
Reduction
A vertex cover of an undirected graph \(G = (V, E)\) is a subset \(V' \subseteq V\), such that each \(e \in E\) is adjacent to at least one \(v' \in V\). Its decision version is to determine whether a vertex cover of at most size \(k\) exists for \(G\).
We can reduce any instance of decision-vertex-cover for \(G = (V, E)\) to an instance of decision-set-cover by letting \(X = E\) and letting the family of sets \(\mathcal{F} = {S_v | v \in V\ \land \text{deg}(v) > 0}\), such that \(S_v\) contains all edges in \(E\) adjacent to \(v\). We can clearly perform this reduction in \(\mathcal{O}(|E| + |V|)\), which is in polynomial time.
We will now prove for any vertex cover \(V'\) for \(G\) and a set cover \(\mathcal{C}\) for sets \(X\) and \(\mathcal{F}\) constructed in accordance with the reduction above:
\[ \exists V'\subseteq V : |V'| \leq k \iff \exists \mathcal{C} \subseteq \mathcal{F} : |\mathcal{C}| \leq k \]
Since \(X = E\), and we know \(V'\) is a vertex cover for \(G = (V, E)\), we can find \(\mathcal{C}\) for \((X, \mathcal{F})\) by selecting from \(\mathcal{F}\) all sets corresponding to \(v' \in V'\).
Similarily, if \(\mathcal{C}\) exists, by the way we defined the reduction, we know it covers \(X = E\). This means We can find \(V'\) by taking the vertices corresponding to \(S_v \in \mathcal{C}\).
Due to the 1:1 correspondence of vertices in \(V'\) and sets in \(\mathcal{C}\): \(|V'| = |\mathcal{C}|~\blacksquare\)
Example
An example is probably useful here. See the image below for an example of a vertex cover of size 4 (with shaded nodes being in \(V'\)).
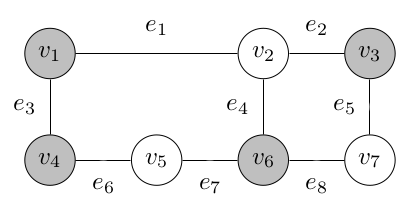
The result of performing the reduction for this example is:
\[ \begin{aligned} \mathcal{F} = \{S_{v_1} &= \{e_1, e_3\}, \\ S_{v_3} &= \{e_2, e_5\},\\ S_{v_4} &= \{e_3, e_6\},\\ S_{v_6} &= \{e_4, e_7, e_8\}\} \end{aligned} \]